There are two parts to this homework: a written component worth 10 points, and a programming assignment worth 15 points. See the homework submission instructions on how to hand it in and for important notes on programming style and structure.

Note: parts in red, if any, are revisions/clarifications.

Written questions

1. (3 points) Given the following graph:
   

   

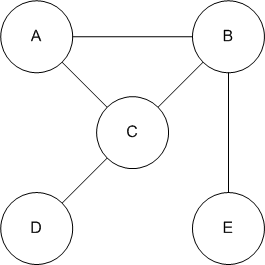
   1. (1 point) Draw an adjacency-matrix and an adjacency-list representation of this graph.
   2. (1 point) List the vertices in the order they would be visited in a BFS and a DFS of this graph starting from vertex A.
   3. (1 point) Specify a spanning tree for this graph. (Use the connected vertices to specify an edge, e.g., AB.)
2. (3 points) Given the following graph:
   

   

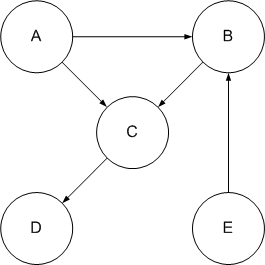
   1. (1 points) List the vertices in topological order. Is this the only topological ordering for the graph? Explain in one or two sentences why.
   2. (2 points) Draw the adjacency matrix for the graph. Compute its transitive closure via Warshall's algorithm, and draw the resulting connectivity matrix. Are there any cycles in this graph? Explain in a sentence why or why not.
3. (4 points) You're given the following list of distances between cities. (Unlike my class examples, these are supposedly real!) You may assume the distances are symmetric.
   • Boston-Buffalo: 400mi
   • Boston-Denver: 1,769mi
   • Boston-New York: 188mi
   • Boston-Washington: 393mi
   • Chicago-LA: 1,745mi
   • Chicago-Denver: 920mi
   • New York-Chicago: 713mi
   • New York-LA: 2,451mi
   • New York-Miami: 1,092mi
   • New York-Philadelphia: 83mi
   • Miami-Philadelphia: 1,019mi
   • Miami-Washington: 923mi
   1. (2 points) Compute the MST of the implied graph. What edges would be included, and what's the total weight (i.e., sum of all the edges in the resulting tree)?
   2. (2 points) Assume these are the only routes offered by our fictional airline. Use Dijkstra's algorithm to find the shortest paths to every city, originating from Denver. You don't need to show all the intermediate steps, but make sure to write out the "parent" of each destination node (e.g., the last city in the path that one flies through to get to the destination).

Programming problem

In this programming assignment, we're going to add graph functionality to the code in HW#5 to build what one may call a "word network". Much more sophisticated versions of this assignment are sometimes used in natural language research to help develop programmatic understanding of written language. We will also reuse the same corpus of text. If you were not satisfied with your HW#5 code, you'll be able to download the solutions on Thursday, November 27th (after everyone's late days are used up) and use it as the basis. If you implemented the extra credit, you can leave it as-is.

In addition to the existing hash table, you will implement a graph to help build this word network and, in particular, determine the "distance between words" (via a breadth-first search, or BFS). The fundamental assumption we will use is to assume that two consecutive words in the corpus are "connected" to each other. For example, at the beginning of the corpus we have the three words "The Project Gutenberg" -- we will assume this implies that "The" is connected to "Project" (in both ways, i.e., "Project" is also connected to "The"), and "Project" is similarly connected to "Gutenberg". We will do this by linking Word objects together (e.g., not using an adjacency matrix or an adjacency lists; one could engineer the use of either as well, but we already have the object infrastructure mostly built).

One important issue you must understand before implementing this graph algorithm is how we will keep track of distance and visited nodes. Simply put, we can combine the two definitions as we're doing our BFS. If distance is set to -1, then we assume a node has not yet been visited. If distance is >= 0, the node has been visited and we know its distance from the initial source from which we started our BFS. As we populate the BFS's queue, we will assign distances from the start node, which will help us keep track of the distance and mark it as visited. Now, here's what you should do:

1. (8 points) Update the Word class to support adjacent nodes:
   1. (1 point) Add two fields to Word: a list of adjacent Word nodes called "adjacents", and an int called distance which will be used in the BFS. Use a Java ArrayList to store the adjacents. It is in the java.util package, and works very similarly to a LinkedList object. The default distance should be -1 (i.e., unvisited). These fields should be private, just like the other ones.
   2. (2 points) Add a new method, called addAdjacency, that takes an object of type Word as its only parameter. Its purpose is simple: it will add the "other" word to our list of adjacents, and will add ourselves to the "other" word's list of adjacents. However, you must first make sure the "other" word doesn't already exist in our list (and vice-versa) -- if it's in the list, don't add it, because duplicates will mess up our graph algorithm.
   3. (5 points) Implement a method called BFS that takes another Word as a parameter and returns the distance to the supplied word from ourselves. It does this by keeping two ArrayLists in addition to the Words' adjacents: one will keep track of visited Words so that we can reset their visited property once we're done, and the other will be the queue used in the BFS algorithm. We will also keep track of the "current distance" (starting at 0). The algorithm works as follows:
      1. First, add ourselves to the queue. This is accomplished by adding ourselves to the end of the queue, setting our distance to zero (since we're adjacent to ourselves), and adding ourselves to the list of visited words.
      2. Now, as long as the queue is not empty:
         • Remove the head of the queue. We'll call this h;
         • If h is the Word we want, note down its distance (this will be the return value) and break out of the loop;
         • If h is not what we want, add h's unvisited adjacents to the queue. This is accomplished by first setting the "current distance" to h's distance plus one (since we're looking at farther-away nodes), and then looking at h's adjacents one-at-a-time:
           • If the ith adjacent of h has been visited (distance >= 0), skip it;
           • Otherwise, add it to the queue. We do this almost the same way we added ourselves: we add the Word that's the ith adjacent of h to the end of our queue, we set its distance to be the "current distance", and add it to the list of visited words.
      3. When we get here, either we have found the optimal distance (and have broken out of the loop) or we've traversed the entire graph and not found the remote Word. The latter should never happen (why?), but in case it does, we'll return -1 as the distance. Otherwise, we'll return the actual distance we found. But first, walk through the list of visited Words, and set their distances to -1 (so that future BFSes work), and then go ahead and return the distance.
2. (7 points) Update the WordHashtable class to support Word's new functionality:
   1. Rename it to WordGraph to avoid confusion with the previous homework.
   2. (1 point) Implement a method called get that takes a String and looks up the corresponding Word in the hash table. If the word doesn't exist, the method should return null.
   3. (3 points) Modify the insert method so that it adds adjacencies via the Word's addAdjacency method. In order to accomplish this, insert itself must be modified so that it takes two parameters: the name of the word being added, plus the name of the previous word (with which this word should implicitly be linked as per the definition of connectivity above). It should then use the get method to get the previous word's reference after the "current" word is inserted, and should mutually call addAdjacency on each of the Words (i.e., adding each Word to each other's adjacency list). In order to keep insert backwards-compatible with previous calls, add an overloaded insert method that takes just the String to be inserted and calls the two-parameter insert, specifying null as the second parameter. (Correspondingly, your two-parameter insert must support handling a null previous word.)
   4. (1 point) Implement a getDistance method that takes two Strings as a parameter, looks up both words using get, and calls the BFS on one and supplies the other as a parameter. (Since our graph is undirected, it shouldn't matter which node you start the BFS from.) You should return the integer value that BFS gives back to this method.
   5. Finally, modify the main method:
      1. (1 point) Change your main() method such that it takes one command-line parameter -- which it then uses as the filename (as opposed to hardcoding tprnc10.txt; if a parameter is not specified, print an error and quit). Normalize all of the input going into the hash table/graph, i.e., convert words to lowercase, strip any symbols or numbers from them, and don't insert any words that consist strictly of symbols/numbers. This is a necessary step because it may materially affect distance.
      2. (1 point) When possible, add the current word and the previous word, as per the new insert method in WordGraph, when you're reading the corpus into memory. The easiest way to do this is to keep a temporary variable that stores the previously tokenized word, and supplies it as the second parameter. Obviously, the first word will not have a "previous" word designation.
      3. Instead of reading one word at the ">" prompt, read two. Use the two words as parameters to getDistance, and print out the distance received back from the method. In the case of invalid words (e.g., a getDistance result of -1), print out "not found or no such path".
3. (5 points extra credit) Implement a new word network that's capable of using Floyd's all-pairs-shortest-path algorithm to build a "distance matrix" of Words.
   1. Don't use the WordGraph class as designed above; instead, build a WordMatrix class that uses an adjacency matrix representation for all the words. Use the book's model, with the array of vertices being Word objects. Make sure to avoid duplicates (linear searches are fine). The initial weight between two adjacent nodes is 1 (i.e., two adjacent nodes are "1" word apart.
   2. Use a main() method similar to the above one: it reads words, normalizes them, and inserts them (and their adjacencies) into the above WordMatrix data structure. Once done, it invokes Floyd's algorithm, which produces a new distance matrix stored in a separate table in WordMatrix. Finally, build a user interface that takes 1 or 2 words: if you are given 2 words, do the lookup in the distance matrix (i.e., produce a result similar to the one the WordGraph tool produces), but if you're given 1 word, look its row up in the distance table (again, a linear search is fine) and return the 10 most distant word pairs between the specified words and other words in the corpus. (You'll have to employ some sort of copy-into-array-and-sort mechanism to do this.)
   As this bonus assignment implies, the design is fairly open-ended. It's not too difficult, but one warning: the above architecture will not easily be able to handle something as large as "The Prince". Instead, find a smaller corpus in Project Gutenberg or another source to use. Something with 500 words is ideal. Talk to me and make sure you're clear on what needs to be done before embarking on this.