Project
3: Cluedo
Group 3
Behrooz Badii
Mark Berman
Prakash Gowri Shankor
Introduction:
In this project, groups were assigned to create players that could guess a set of hidden cards that were in the set of total cards, with the rest of the cards equally divided among all players. This is similar to the game of Clue or Cluedo. One would have to make queries from other players to obtain information, use other players’ queries to obtain more information, and to guess the set of hidden cards as quickly as possible without being wrong. The metric in this problem is how quickly one could obtain a correct guess. In other words, one would have to correctly guess before all other players.
Ideas
and changes:
Our player had as many changes to it as there were name changes (It has been called HARDAC after the computer in the old Batman™ series, Abhinav after our TA, Lestrade, and “I voted for Kodos” referring to a joke in the T.V. show The Simpsons.) The main parts of the program were in making queries, inferring information from other people’s queries, and guessing the hidden set of cards correctly.
Making queries
In this subsection of the problem, there was a consistent pattern of change to more intelligent guessing. The first query algorithm was simple; we would pick a random set of numbers, and if we don’t get a negative result, we wouldn’t ask that number again. That was soon changed to an algorithm where we would ask all the numbers that are known to be absent from that person’s hand and we would also add to that query all the cards whose whereabouts were unknown. However, inferences can be easily made from this algorithm. If the player stops guessing the number 3, then the inference algorithm of another player can realize that the number 3 is not in the hidden set. Therefore, by asking for cards that way, one gives away a very large amount of information. So that algorithm evolved into partially padding the unknown cards with a subset of all the cards absent from that player’s hand. However, one is still asking all the unknown cards for that player. A stronger inference algorithm can notice that these numbers are being continually asked, so they must still be unknown. Hence, the final algorithm was created that asked for the minimum number of unknown cards while still giving our player a positive reply. The algorithm is:
U+Ki-P+1
U = the number of total unknown cards
K = the number of known cards for player i
P = the number of total cards per player
This returns the minimum number of cards a player should ask so as to get a positive result, since getting a positive result, in the average case, gives more information than getting a negative result. This number is the number of unique unknown cards our player asks. However, there is still padding using a subset of cards absent from the hand of the player being queried. After combining the unique unknown cards to be asked and the subset of cards that are absent, we are ready to make a query that always returns a positive result, and the query is seldom the target of a successful query inference.
Inference of information from other players’ queries
Our group did not concentrate extremely heavily on this situation, but we do have a successful query inference engine. This is apparent in the tournament results, which will be discussed in its section. Every query is a disjunction. These disjunctions can and are combined to make larger disjunctions. However, information gathered from our own queries aids to eliminate certain singletons from the disjunction. Through this process, disjunctions can be broken down into manageable singletons, which represent that the person who had been asked either does or does not have the card. In general, this inference engine is weak, since it relies on our own answers to gain more information. However, it was good enough to give us a slight edge over other players so that we could consistently place in higher rankings. The inference engine performs very strongly in an end game situation, where we are looking to single out only a few specific cards.
Making guesses
All the information that’s gathered through queries and through the inference procedure must be compiled. This player uses a list of cards for each player. When a player has that card, it is noted as PRESENT. Therefore, the card cannot be in the hidden list. When a player is known not to have that card, it is noted as ABSENT. This is used for the padding of queries. When a card is found to be present for a player, that card is noted as absent for all other players. If the position of that card is still unknown, it is noted as UNKNOWN. After total information is gathered for all cards not in the hidden set, then the hidden set is fully realized. So the guessing strategy is based on finding all the known cards first. The complement of the final known card set is the hidden set.
Group3Player4:
Group3Player4, also known as “I Voted for Kodos”, formerly known as “Abhinav”, formerly known as “Lestrade”, formerly known as “HARDAC”, uses the final query padding algorithm in querying for guaranteed positive results, uses the inference procedure of breaking lists of queries down to singletons, uses the list of cards for each player data structure, and uses sure guessing to guess the hidden set of cards.
Tournament Analysis:
Here are the results of the tournament. There are two simple ways to interpret the tournament. One way is to take the absolute ranks (an integer from 1 to 9) between players after running their games for each setting and report with them, or one can take the average ranks (a real number from 1 to 9) for each player after running their games for each setting.
First, there are the absolute ranks. In this fashion, we did fairly well. We didn’t do spectacularly like coming in first or second all the time, but we had our share of first and second along with our share of average placing:
|
Our
Actual Average Rank |
Average Absolute Rank for each
combination of Numbers of Players and Cards Per Player |
||||||
|
Number of
Players |
Cards Per
Player |
1 |
2 |
3 |
5 |
8 |
16 |
|
2 |
|
2 |
3.33 |
3.33 |
2.75 |
3.75 |
3 |
|
3 |
|
7 |
4 |
5 |
3.5 |
4 |
3.5 |
|
5 |
|
4.5 |
2.33 |
5.33 |
4.25 |
3.5 |
3.5 |
|
7 |
|
5 |
1.67 |
4 |
3.5 |
2.5 |
3 |
|
9 |
|
5.5 |
1.67 |
3.33 |
3.75 |
3 |
|
|
10 |
|
|
|
3 |
|
|
|
This average absolute rank is in correlation to how well all players did in specific tournaments. For example, in 3 player tournaments, our ranking was 7th (our worst placing) because 6 other players had better ranks than us in the 3 player tournaments they participated in. More importantly, this absolute average rank shows how well our player does with certain game specifications:
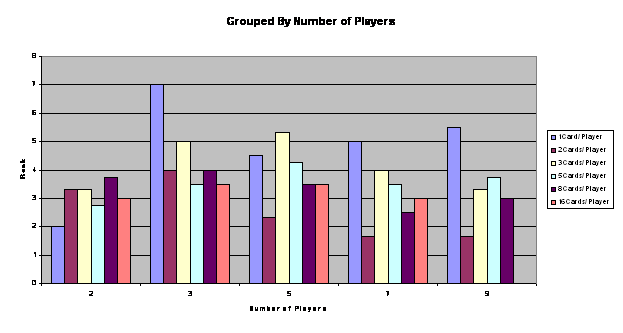
Using this interpretation, one can see that we would do generally do worse with one card with a higher number of players. However, when the number of players is very low or very high, we do well
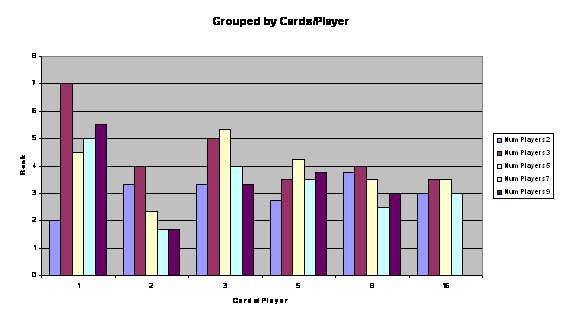
Under this interpretation, we see that we obviously do very badly with only one card per player. However, with 2 cards per player, we do very well. We believe this is due to the disjunction and singleton inference reasoning mechanism, but after 2 cards per player, we start having better and better ranks.
The other way to analyze the tournament is to consider the average ranks for each player. In this situation, it shows that even though our absolute ranks might be good, our average ranks in our own tournaments are a little better:
|
Our
Player |
Average Rank for each combination
of Numbers of Players and Cards Per Player |
||||||
|
Number of
Players |
Cards Per
Player |
1 |
2 |
3 |
5 |
8 |
16 |
|
2 |
|
1.39 |
1.372 |
1.356 |
1.3055 |
1.3275 |
1.34325 |
|
3 |
|
2.068 |
1.791333 |
1.879333 |
1.7555 |
1.85775 |
1.86275 |
|
5 |
|
3.168 |
2.533667 |
2.847 |
2.754 |
2.785 |
2.72275 |
|
7 |
|
4.5935 |
3.291667 |
3.562667 |
3.50375 |
3.4365 |
3.3395 |
|
9 |
|
5.9075 |
3.946 |
3.957333 |
3.76725 |
4.2315 |
|
|
10 |
|
|
|
|
3.534 |
|
|
This table shows that our average rank for our player is near or better than the natural average (for 2 it’s 1.5; for 3 it’s 2nd ; for 5 it’s 3rd ; for 7 it’s 4th, for 9 it’s 5th ; and for 10 it’s 5.5). However, more importantly, is how our average compares to the highest player in each combination.
|
Diff
Between Us and Top Player |
Average Rank Difference for each
combination of Numbers of Players and Cards Per Player |
||||||
|
Number of
Players |
Cards Per
Player |
1 |
2 |
3 |
5 |
8 |
16 |
|
2 |
|
0.0605 |
0.100333 |
0.146 |
0.135 |
0.13425 |
0.1645 |
|
3 |
|
0.396 |
0.121 |
0.353333 |
0.47325 |
0.55525 |
0.62525 |
|
5 |
|
1.3345 |
0.168 |
0.658333 |
0.92075 |
1.2895 |
1.49525 |
|
7 |
|
2.9395 |
0.114667 |
0.497333 |
0.78325 |
1.50575 |
1.905 |
|
9 |
|
4.3465 |
0.100333 |
0.484333 |
0.73175 |
1.5295 |
|
|
10 |
|
|
|
|
0.672 |
|
|
Other than some outliers (4.3465 and 2.9395), our average rank in each combination of the number of players and the number of cards per player were very close to that of the top players. This inherently shows the difficulty of considering a supreme winner, since the margin of difference between all almost all the top players are very close to zero.
As one can see, we have done fairly well in the tournament in all aspects (except for when there is only one card per player or we are up against one player). However, the problem is realizing a clear-cut winner when one sees how close the ranks are to one another. I find it slightly ridiculous to give an absolute rank of 2 to a person only when there average rank for those tournaments was something like .05 lower than that of the 3rd ranked player.
Conclusion:
This project was very interesting. Since there was no need to rely heavily on geometric equations such as in the Cookie Cutter Problem, a person could describe and define their ideas more easily. This lead to stronger class discussions where people had a much easier time of understanding one another while going deep into a detailed description of an idea. For example, the minimum query algorithm was very easy to create and describe since it was intuitive and very little technical knowledge was needed. This reminded us of the Rectangles Revisited problem in a strange way. I would imagine that the first students doing the Rectangles problem felt much like us in this problem. Ideas were easy to implement and test, and there was a visually gratifying race to win in each. We imagine that the continuation of this problem would lead to much more advanced or developed players (just like how our players in Rectangles generally faired well against the old Rectangle players). Three weeks was just not enough time to develop highly complex query inference engines, but we think that if other people had code to start them off (like we did in the Rectangles problem), their primary focus would be the synthesis of a very intelligent inference engine.