- All
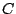 cards known:
cards known:
The first type of inference that we make is when we know all
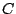 of a player's cards. Then, any cards that are left in the uncertain
set are removed using the ``lacks" assertion. This assertion is
also applied right at the beginning of the game because we know all
of a player's cards. Then, any cards that are left in the uncertain
set are removed using the ``lacks" assertion. This assertion is
also applied right at the beginning of the game because we know all
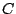 of our own cards; we are able to assert that we don't have the
rest
of our own cards; we are able to assert that we don't have the
rest 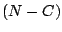 of those cards.
of those cards.
- Card Returned:
The next type of basic inference is in response to an interrogation. When a card is returned we assert that every other player lacks this card.
- No Cards Returned:
Next, we are able to infer from an interrogation result of ``No Cards". From this we are able to assert that the interrogated player does not have any of the requested cards.
The following are inferences we make by looking for information from previous moves. This information is stored in the clause list for each player.
- Single item clause:
We populate a clause with the subset of cards in an interrogation that we are not sure about. That is, if a interrogation consists of a card that we know belongs to someone else, then we do not include it in this player's clauses. Next, if any card is later identified to belong to a player, then any clause in that player's clause list that contains that card is removed. This is done because no more information can be inferred. Similarly, once we identify such a card, we remove that card from all clauses in the other players' clauses disjuncts. Finally, all this pays off when we see a clause with only one card left. This means that we were able to deduce that this card was the one returned during interrogation, and we then assert that this player has this card.
- One card left to discover:
Another clever inference that we make is that if we know that there is only one card left that needs to be discovered for a player, then we take the intersection of all cards in that player's clause list. We assert that the one remaining card must be in this disjunction, and every other card on the uncertain list is not in this player's disjunction.
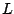 cards left to discover:
cards left to discover:
The last inference that we make is as follows: say we need to discover
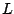 more cards for that player. If we can find
more cards for that player. If we can find 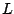 disjoint disjunctions then we can infer that the possible cards that
are not in those disjointed disjuncts do not belong to this
player. This assertion is a more general form of the previous ``One
card left in clause" inference.
disjoint disjunctions then we can infer that the possible cards that
are not in those disjointed disjuncts do not belong to this
player. This assertion is a more general form of the previous ``One
card left in clause" inference.