Group 4 Project Report

Problem Analysis

There are several things to consider while designing a player for "Let's Get Together". These include the general strategic philosphy for single- and multi-player games, conventions for meeting an adjacent player, deadlock handling and prevention, concerns over strategy assumptions in multi-player games, and the usefulness of trail following.

Strategic Philosophy

"Let's Get Together" required a different sort of approach than the previous problems in this course. Most markedly, this problem is one of collaboration, rather than competition. On the other hand, with the division of teams, there grows a desire to design a "better" player than the other teams. This produces a need for finding a balance between designing a player that out-performs others in single-player games, but plays well with others and contributes to the overall performance of a multi-player game.

Meeting Conventions and Deadlocks

A good player needs a convention for meeting an adjacent player, while remaining free of deadlocks. Which player should move toward the other? What happens if neither moves, or if both move? Several conventions were discussed in class.

The easiest convention to implement is the "Higher Move" strategy. In this convention, the player who must make the higher numbered move toward the other is designated the mover. Since the 9 possible moves are uniquely numbered, this convention initially seemed to be straight-forward and clean. However, it is subject to occasional deadlocks when more than one player is involved. For instance, consider the case where the board has width 3, and 3 players are aligned vertically (Fig. 1).

	1
	2
	3

Fig. 1: Deadlock using the "Higher Move" convention

Here, player 1 sees player 2 to the south and player 3 to the north. Say player 1 decides to try to meet player 2. Since player 1 would have to move south (direction 4), and player 2 would have to move north (direction 3), player 1 considers himself to be the one expected to move. However, say player 2 decides to meet player 3, and player 3 decides to meet player 1. Using the same reasoning, players 2 and 3 also decide they must move south. This causes a deadlocked loop with all three players chasing one another. On the other hand, if they all decided to meet the players to their north, each would decide to wait, creating a stagnant deadlock. In any case, a player who uses the "Higher Move" meeting convention, must have a way to solve or break this type of deadlock. This could be done by complicating the move-or-stay decision process, by implementing rules to detect and break deadlocks, or by implementing a timeout for meeting attempts.

Another meeting convention of interest discussed in class was the "Opposing Ls" convention. In this convention, the neighboring squares around a player were divided into two Ls, as in Fig. 2.

	.
	1
.

Fig. 2: The "Opposing Ls" convention

In this convention, if an adjacent player is in, say, the lighter L, the player is to move, and otherwise stay put. This convention, however, is subject to the same deadlock concerns as the "Higher Move" convention and is more difficult to implement, so we ultimately rejected it.

Strategy Assumptions

In a single-player game, each player is using the same strategies and conventions. In a multi-player game, each player may be using a meeting convention that is orthogonal to one's own. There is no way to tell whether the current game is single- or multi-player without observing extensive play of the game. For this reason, it is important not to make any hard-lined assumptions about the strategies and conventions of the other players on the board. Each player must be prepared to avoid, prevent, or break any deadlocks that may arise from opposing strategies and conventions.

Trail Following

An initial reaction to "Let's Get Together" might be that following the trails on the board could be highly useful. Indeed, trail following is useful, but only under certain board conditions. One of the main problems with following trails is that the trails do not degenerate over the course of the game. That is to say, trail information indicating the passage of information unit 2 through a cell tells a player only that unit 2 has been there at some point over the course of the game. Given the above conjecture that no assumptions can be made about the strategies of other players on the board in a multi-player game, it can be said that trail following is more useful in a single-player game, when one can be sure that the other players are using the trails in a similar way. In a multi-player game the trails cannot be fully trusted. Additionally, as the game progresses, the board becomes increasingly "dirty" with trails from earlier parts of the game. Therefore, in order to make good use of trails, the trails must be planned and utilized wisely.

It is important to note an initially discussed "Optimal Strategy" here. Bogdan Caprita suggested in class that one player could move in a set horizontal or vertical direction, while all others would move perpendicular to it. This first player would act as an information collector, and the others would simply seek it out by its trail. If the players knew their player numbers, as they initially did, "Let's Get Together" was reduced to a simple solution with an upper bound of 2L + 2W moves before convergence, as the player numbered 0 (for instance) could always be designated the collector. Because this made the problem less interesting, the class voted to mask the player numbers from the players themselves, such that each player considered himself player 0 and had a unique player number mapping for the others on the board. This hindered any strategies that required one designated player to perform a special role.

Strategies

Salsa y Arroz

Salsa y Arroz was the first player we developed. We were motivated to create a player that used little random movement and that laid stable horizontal and vertical tracks in order to find the other players. Noticing that chasing each other on the tracks was likely and counter-productive, since the players all move at the same speed, we also wanted to find a way for the tracks to be used without producing a loop with no chance of convergence. For this, we recognized the need for slowing or stopping on a trail we knew another would travel.

Each instance of Salsa y Arroz first randomly chooses to move horizontally or vertically, with a small bias toward the shorter direction. Those players moving in the shorter direction search for trails that span the longer direction. When they find a trail, they wait for the player who laid it to return for a number of moves equal to the longer direction. If a player does not gain any new information in that number of moves, it changes to the perpendicular direction with probability 0.5. It will always try to meet an adjacent player that is has never seen, and will meet a player it has seen with a 0.2 probability. Salsa y Arroz uses the "Higher Move" convention for meeting.

Salsa y Arroz performs decently alone, but is subject to a few drawbacks. First, it has no deadlock prevention or detection strategies, so it occasionally gets stuck making no movement or following non-converging loops. Second, a dirty board will ruin the strategy, so it does not perform well with players that do not follow a similar horizontal/vertical trail-following strategy.

Hybrid

Hybrid was the second player we developed, partially in response to the large number of horizontal and vertical movers we saw in class. We also noticed that while horizontal and vertical movement was indeed popular, not everyone followed this pattern. Since not following this pattern dirties the board for trail following, we decided that covering as much of the board as possible might be a better strategy. As a result, Hybrid exploits a spiral movement to cover an area of the board for a portion of time, then moves away from its location and begins the spiral again.

Hybrid moves in a diamond spiral, so as to uncover more cells with each move. When each move is diagonal, rather than horizontal or vertical, 5 new cells are seen, instead of only 3, as shown in Fig. 3.

.
.
.				2
.	1	1	2
.
.

Fig. 3: Diagonal movement uncovers more new cells. Light grey indicates previously seen cells, dark grey indicates newly uncovered cells.

Hybrid starts by choosing a random diagonal direction and moves one cell in that direction. It subsequently turns in the perpendicular direction, going clockwise, and moves one cell further than it did going the past direction. It keeps track of the number of rounds it has moved since gaining new information, and continues moving in its spiral until it has moved a number of rounds proportional to the area of the game board without gaining new information. Through experimention, we found the optimal number of moves was 25% of the area for boards with area greater than 1000, and 33% of the area otherwise. After moving this number of rounds, Hybrid picks a random direction and moves in that direction a number of moves equal to 25% of the longer of the two sides of the board, then begins a new spiral. If at any point Hybrid is adjacent to another player, it attempts to meet it. If Hybrid acquires new information in a meeting, it restarts its spiral motion from there. Otherwise, it continues its previous movement.

Hybrid uses the "Higher Move" meeting convention. In order to prevent deadlocks, it follows these rules:

If it is trying to meet another player and determines itself to be the one to wait, it waits one turn. If this does not result in meeting, it times out and moves toward the other player, if the other player is still there. If the player has moved away, it continues its spiral.
If it is trying to meet another player and determines itself to be the one to move, it moves one turn. If the result is a location trade, it stops and waits for the other to come back for two turns. If the meeting has still not taken place, it times out, moves one cell in a random direction, then continues its spiral. It should be noted here that there remains the possibility of a degenerative case, in which Hybrid continues meeting the same rogue player despite moving one cell away. In this case, there is a deadlock-timeout cycle. However, this cycle is broken when Hybrid has moved a number of moves without gaining information, as mentioned above, in which case it moves away from the area and restarts its spiral.

This deadlock resistence is one of Hybrid's best virtues. While we are sure there are more elegant ways to resist deadlock than timing out, we find this method to be quite effective.

We found Hybrid to be particularly good for multi-player games for a number of reasons. First, its spiral motion covers the board well, so it often finds other players who might be in deadlock in a remote part of the board. Second, it is not dependent on others' strategies in order to contribute to the goal of the game. Finally, since it does not employ trail following, it is not dependent on clean trails, and, therefore, is not distracted by a dirty game board.

In single-player games Hybrid performs less well. While it usually makes a decent run, scoring less than 1000 for any reasonably sized board, it has no upper bound on the number of moves. In fact, when playing alone, it is sometimes caught playing more than 5000 rounds, showing no signs of convergence.

Overall, though it is unpredictable and defies a deterministic upper bound for convergence, we were fairly pleased with Hybrid's performance.

Groovy

We submitted Groovy as Group4Player1 in the class tournament. Groovy is a highly probabilistic player, and its movement can be described as controlled randomness. With Groovy, we attempted to expand on Hybrid's board coverage with an eye toward optimizing performance in multi-player games. Groovy begins by moving in a saw-tooth fashion in the direction of the longer side of the board. This pattern can be seen in Fig. 4.

.
.	1		1		1		1		1
.		1		1		1		1
.

Fig. 4: Groovy's saw-tooth movement.

The saw-tooth pattern was chosen so as to give Groovy a wider view of new cells. After moving a number of moves equal to the larger of the two board sides (call this distance G), Groovy will begin to move perpendicular to its previous direction if it has gained any information, or begin a spiral motion if it has not. When the arm of the spiral is equal to G, Groovy will revert back to the saw-tooth pattern.

Whether moving in the saw-tooth or spiral pattern, Groovy will always attempt to move toward an adjacent player it has never seen with probability 0.75. If it has met an adjacent player before, but has not seen it in 3 or more moves, it will move toward it with probability 0.5. If Groovy does not determine the presence of an adjacent player, it will check for the presence of a trail. If it is on a trail of information it lacks, it will wait for a number of rounds. This wait time is determined as follows:

The maximum wait time T is set at 2G
A coefficient C is calculated such that C = N/A, where N is the number of players, and A is the area of the board
The wait time is calculated based on the value of C. These values were obtained through experimental results:
- If C > 0.025, then wait = T
- If 0.025 > C > 0.016, then wait = T/2
- If 0.016 > C > 0.0042, then wait = T/4
- If C < 0.0042, then wait = T/8
If the resulting wait is less than 3, then wait = 3

Once Groovy has waited its wait amount, it will revert back to its previous movement.

Groovy's probabilistic movement creates a player somewhat resistent to deadlocks. At all times, there is some probability that Groovy will break whatever pattern of action it is currently executing. Groovy also extends Hybrid's beneficial wide board coverage. We found that Groovy works well in a multi-player environment because of its coverage of the board and resistence to deadlocks. For further analysis of Groovy's performance, see "Tournament Analysis".

FlowerOrBee

FlowerOrBee is our attempt to make a horizontal and vertical moving player that is more predictable than any of our previous players and that allows us to make more intelligent estimates of an upper bound to convergence. This player was modeled partially after the "Optimal Strategy" discussed in class. Each instance of FlowerOrBee can be a "flower", with probability 1/N, where N is the number of players on the board. Otherwise, it is a "bee". The aim is to have one flower in a game. The flower's job is to travel along the width or length of the board one time, laying a trail across one row or column. The flower stops once it has returned to its initial position. It then waits for the others to find it. The bees are to find the flower's trail, then follow the trail to meet the flower. Once a bee meets a flower, the bee continues its previous movement. We had two versions of FlowerOrBee.

In FlowerOrBee v.1, flowers always traveled west, and bees always traveled south. Both flowers and bees would wait 2W + L rounds to meet up with another player. If they did not meet another player in that time, they would possibly switch roles, with the probability 1/N of becoming a flower. No meeting convention was needed for FlowerOrBee v.1, since the flowers were stationary after laying their trails, and it was always up to the bees to find and move to the flowers. Because of this, there was also no need for deadlock handling.

FlowerOrBee v.1 usually performed very well when there was at least one flower. If there was exactly one flower, convergence was guaranteed and expected an upper bound of 2W + L. However, when W was greater than L, performance suffered, as a result of the 2W + L wait. Performance deteriorated with differing player role assignments. The more flowers there were, the higher the bound of convergence, as the bees need an extra W + L to find each additional flower. This is compounded by the fact that a flower has an (N-1)/N chance of turning into a bee after 2W + L rounds of not being met. The degenerate case was when the initial (and subsequent) assignments were all bees or all flowers. In these cases, 2W + L moves were wasted either as flowers waited for non-existent bees to show up, or as bees traveled the board in parallel, looking for non-existent flowers. While the "All Flowers" scenario is somewhat unlikely, as the probability of this situation is (1/N)^N, the "All Bees" situation was more likely, with a probability of ((N-1)/N)^N.

We submitted FlowerOrBee v.2 as Group4Player3 for the class tournament. With FlowerOrBee v.2, we attempted to solve some of the drawbacks of FlowerOrBee v.1. In v.2, the flowers choose to travel along the shorter of the two board sides (call this distance F), in hopes that the flower can lay its trail faster, thereby letting the bee find it faster. In addition, the bees travel not only in the two directions perpendicular to the flower (call this perpendicular distance B), but in the diagonal directions as well. Bees choose their directions randomly. By moving in diagonals, the bees have a better chance of meeting independently of a flower, making the "All Bees" situation less detrimental to overall game performance. With exactly one flower, the upper bound on convergence is 2B + F moves, though the diagonal movement of the bees usually produced much earlier convergence. One might ask why the flowers would not travel the longer distance, as this would reduce the 2B + F threshold. Through our experiments, we concluded that this did not make much, if any, difference. Again, this is likely due to the benefits of diagonally moving bees.

We were extremely pleased with the performance of FlowerOrBee v.2, especially in single-player games. FlowerOrBee v.2 maintained v.1's lack of deadlocks, while improving on the rate of convergence. It is helpful in multi-player games, as its role-switching algorithms help the distribution of information. It performs especially well with other horizontal and vertical moving players, as it utilizes the trails left by these players. For further analysis of FlowerOrBee v.2's performance, see "Tournament Analysis".

Cra-Z-y

We were motivated to develop Cra-Z-y as a player that uses learning strategies to prevent deadlocks. It was designed to work in a single-player environment.

Cra-Z-y's movement pattern is a Z-like path. The player travels for some time in horizontal direction and, after the passage of some time, the player takes a diagonal path, opposite to the direction of the initial horizontal direction, ensuring a definite change in direction. It does not rely on trails at all, but aims to cover the board.

Cra-Z-y's meeting convention intends to learn and understand what the player should do, given previous interactions. When it encounters exactly one player it has not met before, it follows the reciprocal of the "Higher Move" convention. That is, instead of the player with the higher move, the player with the lower move is expected to move. When it encounters more than one previously unmet players in adjacent cells, it stays put, hoping that at least one of the adjacent players moves toward it. It is biased toward players that have never been met.

In most cases, Cra-Z-y converges. However, consider the case where all Cra-Z-y players are surrounded by more than one equal priority player. This results in a situation in which all players stay put indefinitely. To solve this, Cra-Z-y may stay put for a maximum of three rounds (this number is randomly chosen to be small). After the completion of 3 rounds, it learns that it is in a sort of deadlock and begins to travel in the opposite direction of expected movement with a 0.5 probability. [Note: There are many cases for which you can have the player behave and learn differently]

Since, Cra-Z-y was focused on deadlock handling, it did not focus on performance optimization. Its poor performance prevented us from submitting it. The effort here was to develop the brain of a player that based decisions on "intuitions", since it could not communicate with other players. Based on the results of previous actions, it learns to behave beneficially in similar situations in the future. It tries to figure out the meeting conventions of the other players and follows that convention the next time it is encountered. We believe it would be interesting to further investigate adaptation strategies.

Tournament Analysis

We submitted two players: Groovy (Group4Player1) and FlowerOrBee (Group4Player3). Groovy was aimed to optimize multi-player games, while FlowerOrBee was aimed at the single-player environment. The results, as we shall see, make it clear that our players did as expected and, in some cases, exceeded expectations.

The tournament was conducted on several boards with differing area. Each set of games was played with differing numbers of players on the boards. In addition, some sets of games were played in multi-player mode, and some were played in single-player mode.

Multi-player Analysis

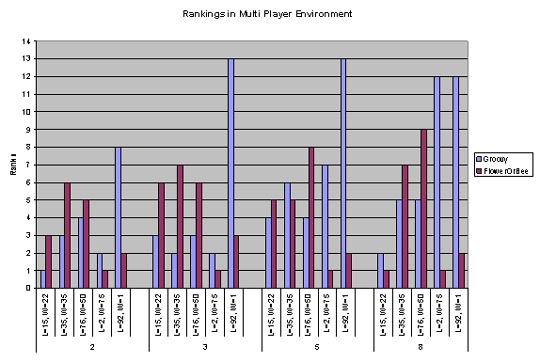
Refer to Fig 5 for the results of the multi-player tournaments. The figure shows performance of all players across the different tournament scenarios. Each cluster of four bars represent games with 2, 3, 5, and 8 players, respectively, from left to right. The performance of Groovy (Group4Player1) was as expected. It can be seen that in severely lopsided boards (2 x 75, 92 x 1), irrespective of the number of players on the board, Groovy's performance was good, as it did better than most players on the board. On the small to medium sized boards ( 15 x 22, 35 x35 ), Groovy's performance was better than more than 50% of the other groups. Only the players from Group 1 and Group 2 matches or betters Groovy's performance. On large sized boards, we did not do as well as expected, however Groovy still did better than 50% of the other groups, and the players of Group 2 and Group 3 did better than Groovy. Additionally, we find that the number of players on the board did not significantly affect the performance of Groovy.

Fig. 5: Multi-player game comparison among the different players.

The performance that surprised us was that of FlowerOrBee (Group4Player3). We expected this player to excel in single-player games (and, as we will discuss later, it did), but from the tournament data for multi-player games, it can be seen that FlowerOrBee's performance is comparable to that of Groovy, which was intended for multi-player games. We attribute this good performance to the fact that FlowerOrBee does not stay put endlessly if no information is seen, but rather, the flower changes roles to become a bee. As a bee, it covers the board well and shares information with other players. While in the bee lifecycle, the player also follows trails, and since there are a few groups in the class that follow and/or leave trails, they all work fairly well together. Also, on a board with many players, being a flower can actually contribute to sharing information, since more players will come across the flower.

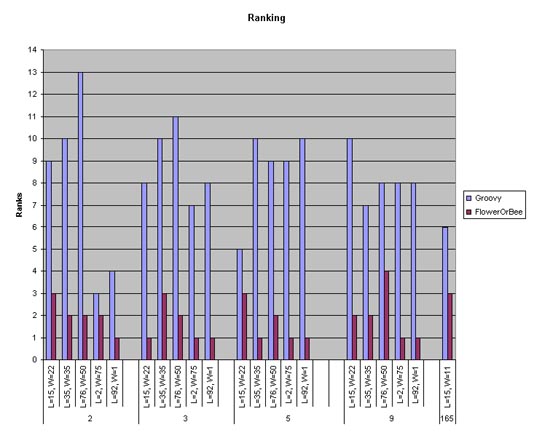
Refer to Fig. 6 for a comparison of the rankings of our two players in multi-player games. Again, it was surprising to see FlowerOrBee perform so well in this environment. Groovy did not perform as well as some other groups, but the difference in the average scores was actually somewhat small. On the other hand, when Groovy was in a multi-player game that performed well, the score difference was significant.

Fig. 6: A comparison of our players' performance rankings in single-player games.

Single-player Analysis

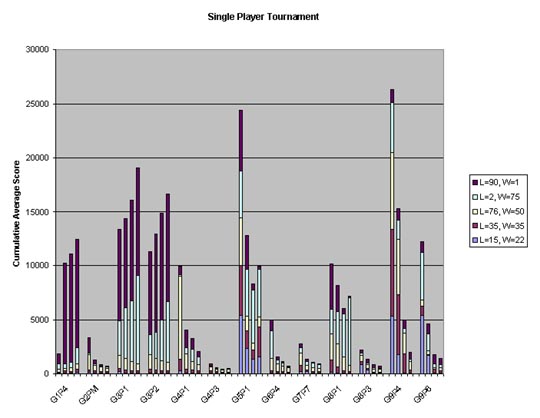
No surprises here; FlowerOrBee dominates the results. Refer Fig. 7 for a comparison of our players' rankings in single-player games. Our method for computing the rankings were for the player with the least average score for each tournament to be ranked 1st, and the one with the highest to be ranked last of the 13 players. FlowerOrBee consistently ranks among the top 3 players in single-player games. In the only exception, it ranked 4th. FlowerOrBee was ranked 1st nine times, 2nd seven times, and 3rd four times. We think the exception case could be due to the occurence of the degenerate repeating "All Bees" or "All Flowers" situations.

Fig. 7: A comparison of our players' performance rankings in single-player games.

Fig. 8 shows a comparison of all players in the single-player tournaments. Each cluster of four bars represent games with 2, 3, 5, and 9 players, respectively, from left to right. As can be seen from the chart, FlowerOrBee (Group4Player3) contributes the shortest set of bars on the chart, signifying the fact that FlowerOrBee has the least average, and thus the best overall performance in single-player tournaments. FlowerOrBee performed exceptionally well under all circumstances. We give some credit for FlowerOrBee's performance to the fact that we partially modeled its strategy on the "Optimal Strategy" discussed in class. This is particularly notable, given the steps taken in class at the start of this problem to prevent such a strategy from being developed and deployed.

Fig. 8: Single-player game comparison among the different players.

Project 3: Let's Get Together

CS4444, 15 November 2004

Introduction

Problem Analysis

Strategies

Tournament Analysis

Conclusions

Team Member Contributions